Periodic Regularities
Here is a physical description of what happens in a watersound-image. That is not an explanation of why it happens.
Vibration
The generative oscillation that causes the process of watersound-images, is technically realized by a loudspeaker, on which a cup, bowl or dish with water is placed.
The conus of this speaker moves up and down, at a chosen number of times per second (the frequenty), and at a chosen height and dept (the amplitude, loudness). Mostly is used a sinus-movement, although it also works with a block wave.
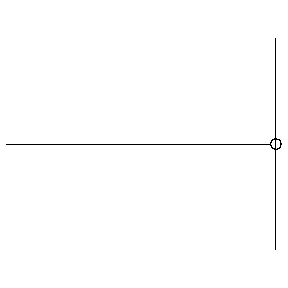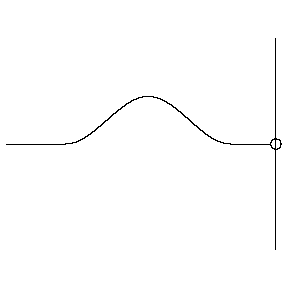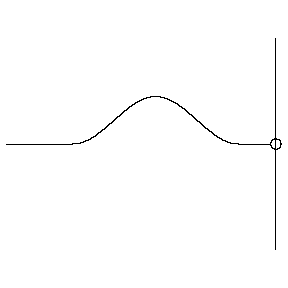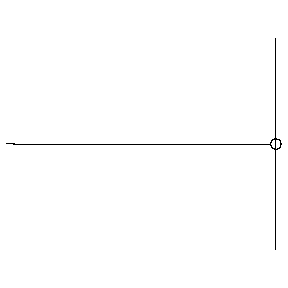
You can feel what a sinus is at the playground on a swing: after you are pulled up, from above you begin falling down, accelerating untill the lowest position, move further in a decelerating velocity, until you stop at the highest position. Then you fall back, speeding up and then slowing down, stop, accelerating and decelerating, stop, etcetera. Children would like going on for ever, repeating the same, in a ritmic way.
You felt a periodic phenomena: a repeated alternation between two polar situations. Between forward and backward, high and low, moving and standing still, speeding up and slowing down… A pure sinus-experience you can also have when you float on or in the seawater…
Concentric circles
The water reacts on this vertical impulse by forming horizontal waves. In the middle of our cup rises a hill, that sinks down to a deep depression. The hill is moving outward as a circular ridge, followed by a similar dept. A crest is followed by a through, which in turn is followed by the next ringvalley, a next ringridge. This repeats again and again, a series of concentric circular waves moves outwardly.

Reflection
Then they reach the border of the water, your cup. What happens when waves meet a boundary? They bounce back (we’ll not focus on diffraction, transmission or refraction here).
Because the process started right in the middle of our cup (not randomly elsewhere), and because the circles stay perfectly round and centric (not eccentic), the circlewave meets the circular boundary with each part at the same time. And then rebounce in a perfectly circular form.
After that reflection they start travelling inwardly. But not just like that!
Phase change
For in the reflected pulse there is a notable phenomena: the wave is inverted, she undergoes a phase change. A crest will return as a trough, a depression reflects as a hill (or better: a circular ridge). Just like at the fixed end of a string, and in the closed end of a wind instrument.
Even swimmers do the same when they reach the end of the swim lane: they bounce against the border, rolling over or under (=inverse) to swim back. Probably they follow intuitively the water's way wich does this spontanuously?
Interference
Those inwardly travelling concentric waves will meet of course the still outwardly moving ones. When two waves meet up with one another, they will influence each other, interact. Two crests will produce a higher crest, two troughs will form a deeper depression, but a through and a crest will neutralize each other.
After the meeting of opposite moving waves, each of them continue following his own path like before the interference, undisturbed, unchanged, as if nothing happened!
Fast moving heads should meet otherwise, unless they kiss each other of course, that should look more like waves do, indeed.
Standing waves
for more info see at http://en.wikipedia.org/wiki/Standing_wave .
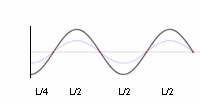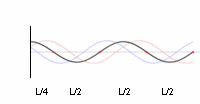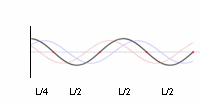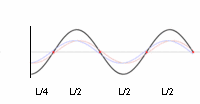
Depending on the relative strength of both waves, the resulting interference-wave will move slowly or fast in one or the other direction. When both are equal, the new wave will look as if she stands still.
Notice that in the standing waves there is a pulsating swing of crests and troughs, (all) crests sink while (all) the neigbor troughs rise, so they all alternate with one other.
According to Cora Tanou in Klangfiguren standing waves will happen when the proportion between the wave-length and the size of the watersurface - diameter is a whole number (if I understand well, this is for specialists).
Anyway, in the experiment you can look for it, by searching the right frequenty (and loudness to make it visible).
What happens when the ringwaves meet the centre?
The outward moving waves that bounced to the outside boundery did not disappear, but turned back and travelled inwardly; the meeting with their opposite travelling waves did not destruct them.
So what will happen when they concentrate in the centre? Will they move on, and grow outwardly again?
Let us look closer into the center of this movie... Use the arrows to follow the moving of the three points arround the midpoint.
Could this be inverted, is the centre-point an inversionpoint? In odd-numbered polygons it looks like that, but in even-numbered ones it looks otherwise. This difference between even and uneven fascinated already people in early times...
Water-behaviour
Even if we let the loudspeaker go up and down as a block-wave, that is without accelerating and decelerating, the water will nevertheless respond with sinusoidal waves. With speeding up and slowing down movements.
A sinus is related with the circle, in fact he is generated by a circle. When you move on a circle at a constant velocity, while projecting your position on a diameter, this projection will oscillate like a sinus.
Water is always behaving “round”:
- a drop that is not influenced by any force (in a spaceship for example) is a perfect ball;
- water flows meandering (even in straight tubes!) , like the Gulf Stream, who even sends out ringform eddies;
-processes happen in cycli.
The round form of our cup is essential to create those beautiful forms and movements. In a square completely other figures will appear, as Hans Jenny showed.